11. 概率图模型PGM

文章链接

https://gitee.com/fakerlove/machine-learning

11.1 隐马尔可夫模型

参考文章

https://www.cnblogs.com/pinard/p/6945257.html
https://www.cnblogs.com/pinard/p/6955871.html

参考资料2

https://www.cnblogs.com/bigmonkey/p/7230668.html

参考资料3

https://www.zhihu.com/question/20962240

参考资料4

https://zhuanlan.zhihu.com/p/95986693

11.1.1 前期准备

隐马尔可夫模型（Hidden Markov Model，HMM）是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。

什么样的问题需要HMM模型????

首先我们来看看什么样的问题解决可以用HMM模型。使用HMM模型时我们的问题一般有这两个特征：

• 我们的问题是基于序列的，比如时间序列，或者状态序列。
• 我们的问题中有两类数据，一类序列数据是可以观测到的，即观测序列；而另一类数据是不能观察到的，即隐藏状态序列，简称状态序列。

有了这两个特征，那么这个问题一般可以用HMM模型来尝试解决。这样的问题在实际生活中是很多的。

比如：我现在在打字写博客，我在键盘上敲出来的一系列字符就是观测序列，而我实际想写的一段话就是隐藏序列，输入法的任务就是从敲入的一系列字符尽可能的猜测我要写的一段话，并把最可能的词语放在最前面让我选择，这就可以看做一个HMM模型了。再举一个，我在和你说话，我发出的一串连续的声音就是观测序列，而我实际要表达的一段话就是状态序列，你大脑的任务，就是从这一串连续的声音中判断出我最可能要表达的话的内容。

从这些例子中，我们可以发现，HMM模型可以无处不在。但是上面的描述还不精确，下面我们用精确的数学符号来表述我们的HMM模型。

1) 马尔可夫模型

a) 例子

先来看一个例子。假设几个月大的宝宝每天做三件事：玩（兴奋状态）、吃（饥饿状态）、睡（困倦状态），这三件事按下图所示的方向转移：

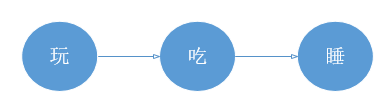
这就是一个简单的马尔可夫过程。需要注意的是，这和确定性系统不同，每个转移都是有概率的，宝宝的状态是经常变化的，而且会任意在两个状态间切换：

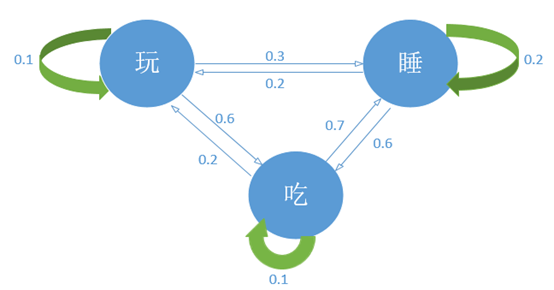
上图中箭头表示从一个状态到切换到另一个状态的概率，吃饱后睡觉的概率是0.7。

从上图中可以看出，一个状态的转移只依赖于之前的n个状态，当n取1时就是马尔可夫假设。

b) 数学解释

马尔科夫过程的定义

马尔可夫过程（Markov process）是一类随机过程。

若随机过程$\{X(t),t\in T\}$​​满足马尔可夫性，则称为马尔可夫过程。

马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。

马尔可夫过程的大概意思就是未来只与现在有关，与过去无关。

马尔可夫链的定义

马尔科夫链（Markov）是最简单的马氏过程，即时间和状态过程的取值参数都是离散的马氏过程。

马尔可夫链是随机变量$S_1,\cdots,S_t$​的一个数列（状态集），这些变量的范围，即他们所有可能取值的集合，被称为"状态空间"，而$S_t$​的值则是在时间t的状态。

如果$S_{t+1}$​对于过去状态的条件概率分布仅是$S_t$​的一个函数，则：$P(S_{t+1}=x|S_0,\cdots,S_t)=P(S_{t+1}=x)$​

这里小$x$​​为过程中的某个状态。上面这个等式称为马尔可夫假设。

上述函数可以这样理解：在已知“现在”的条件下，“将来”不依赖于“过去”；或“将来”仅依赖于已知的“现在”。

即$S_{t+1}$只于$S_t$有关，与$S_{t-n},1<n<t$无关。

c) 转移矩阵

一个含有$N$​​个状态的马尔可夫链有$N^2$​​个状态转移。

每一个转移的概率叫做状态转移概率 (state transition probability)，就是从一个状态转移到另一个状态的概率。

这所有的$N^2$​​个概率可以用一个状态转移矩阵来表示：

$A=\begin{bmatrix}玩&吃&睡\\ 0.1&0.6&0.3&玩\\ 0.2&0.1&0.7&吃\\ 0.2&0.6&0.2&睡\end{bmatrix}$​

随意选取一行，数据为例

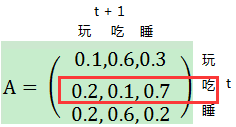
这一行数据表示，如果在$t$时间时宝宝的状态是吃，则在$t+1$时间状态是玩、吃、睡的概率分别为$(0.2,0.1,0.7)$。

矩阵的每一行的数据累加和为1。

2) 隐马尔可夫模型

a) 例子

在很多时候，马尔可夫过程不足以描述我们发现的问题，

例如我们并不能直接知晓宝宝的状态是饿了或者困了，但是可以通过宝宝的其他行为推测。

如果宝宝哭闹，可能是饿了；

如果无精打采，则可能是困了。

由此我们将产生两个状态集，一个是可观测的状态集O和一个隐藏状态集S，我们的目的之一是借由可观测状态预测隐藏状态，为了简化描述，将“玩”这个状态去掉，让宝宝每天除了吃就是睡，这也是大多数家长共同的愿望，模型如下：

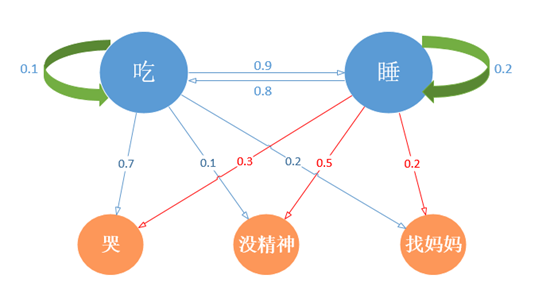
由此得到$O=\{O_{哭},O_{累},O_{找妈妈}\}$,$S=\{S_{吃},S_{睡}\}$​​​。

宝宝在"吃(饥饿)"状态下表现出哭、没精神、找妈妈三种可观察行为的概率分别是$(0.7,0.1,0.2)$​。

上面的例子中，可以观察到的状态序列和隐藏的状态序列是概率相关的。

于是我们可以将这种类型的过程建模为有一个隐藏的马尔科夫过程和一个与这个隐藏马尔科夫过程概率相关的并且可以观察到的状态集合。这就是隐马尔可夫模型。

隐马尔可夫模型 (Hidden Markov Model，HMM) 是一种统计模型，用来描述一个含有隐含未知参数的马尔可夫过程。

通过转移矩阵，我们知道怎样表示$P(S_{t+1}=m|S_t=n)$,怎样表示$P(O_t|S)$​,呢（观测到的状态相当于对隐藏的真实状态的一种估计）？在HMM中我们使用另一个矩阵：

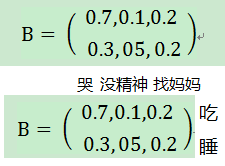
该矩阵被称为混淆矩阵。矩阵行代表隐藏状态，列代表可观测的状态，矩阵每一行概率值的和为1。

其中第1行第1列，$P(O_{哭}|P_{吃})=0.7$​，宝宝在饿了时，哭的概率是$0.7$​。

b) 数学解释

一个HMM可用一个5元组$\{O,S,\pi,A,B \}$​​表示，其中：

名称	解释
$\pi$	$\pi={\pi_i}$为初始状态概率；代表的是刚开始的时候各个隐藏状态的发生概率；	$\pi_i$表示$t=1$时刻状态为$q_i$的概率
$A$	$A=\{a_{ij}\}$为隐藏状态的转移矩阵；$N*N$维矩阵，代表的是第一个状态到第二个状态发生的概率；	$a_{ij}=P(S_{t+1}=q_j
$B$	$B=\{b_{ij}\}$为混淆矩阵，$N*M$矩阵，代表的是处于某个隐状态的条件下，某个观测发生的概率。	$b_{ij}=b_{S_j}(O_i)=P(O_i
$O$	观测序列$O=\{O_1,O_2,...O_T\}$	$M$表示可观测状态的数量，可以通过训练集获得；
$S$	隐藏序列(状态序列)$S=\{S_1,S_2,...,S_T\}$	$N$表示隐藏状态的数量，我们要么知道确切的值，要么猜测该值；

在状态转移矩阵和混淆矩阵中的每个概率都是时间无关的，即当系统演化时，这些矩阵并不随时间改变。

对于一个N和M固定的HMM来说，用$\lambda =\{\pi, A, B \}$​​​​​​表示HMM参数。

c) 两个假设

隐马尔可夫模型需要遵守一下两个假设，只有在这两个假设条件下，才能去求解一些问题

齐次马尔科夫假设

$$P(S_t|S_{t-1},O_{t-1},\cdots,S_1,O_1)=P(S_t|S_{t-1})$$

假设某一时刻状态转移的概率只依赖于它的前一个状态。

观测独立性假设

$$P(O_t|S_T,O_T,S_{T-1},O_{T-1},\cdots,S_{t},O_{t},\cdots,S_1,O_1)=P(O_t|S_t) \\ P(O_t,S_t|S_{t-1})=P(O_t|S_t)P(S_t|S_{t-1})$$

混淆矩阵可视为马尔可夫模型的另一个假设，独立性假设

独立性假设：假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其它观测状态无关。

即$S_{t-1}$和$O_t$之间独立作用$S_t$

3) HMM观测序列的生成

输入的是HMM的模型$\lambda=(A,B,\pi)$,观察序列的长度$T$

输出是观测序列$O=\{O_1,O_2,\cdots,O_T\}$

生成的过程如下

1)根据初始状态概率分布$\pi$​生成隐藏状态$S_1$​

2)for t from 1 to T

​ a. 按照隐藏状态$S_t$​​​的观测状态分布$b_{i_t}(k)$​​​生成观察状态$O_t$​​​

​ b. 按照隐藏状态$S_t$​​的状态转移概率分布

所有的$O_T$一起形成观测序列$O=\{O_1,O_2,\cdots,O_T\}$

4) HMM模型的三个基本问题

HMM模型一共有三个经典的问题需要解决：

问题描述	人话解释	数学解释	解决办法
评估观察序列概率。	已知整个模型，宝宝的行为依次是哭 -> 没精神 –>找妈妈，计算产生这些行为的概率。	即在已知一个观察序列$O=\{O_1,O_2,\cdots,O_T\}$，和模型$\lambda=\{A,B,\pi\}$的条件下，观察序列O的概率 计算在模型$\lambda$下观测序列$O$出现的概率 $P(O	\lambda)$。
模型参数学习问题。	通过宝宝的行为，哭、没精神、找妈妈，来确定宝宝的状态转换概率。	给定一个观察序列$O=\{O_1,O_2,\cdots,O_T\}$，估计模型参数$\lambda=(\pi, A, B)$参数，使得$P(O	\lambda )$最大
预测问题，也称为解码问题。	已知整个模型，宝宝的行为依次是哭 -> 没精神 –>找妈妈，计算这三个行为下，宝宝的状态最可能是什么。	已知模型参数和可观察状态序列，怎样选择一个状态序列$S={S_1,S_2,…,S_T}$，能最好的解释观测序列O。	维特比算法

好了，对应上面的三个问题，分别有三个算法求解对应的问题。

1. 概率计算-前向后向算法
2. 参数学习-最大似然估计（有监督），Baum-Walch（无监督）
3. 预测-Viterbi算法

11.1.2 算法推导

1) 概率计算

问题描述

我们已知HMM模型的参数$$\lambda ={\pi, A, B }$$​。其中$A$​是隐藏状态转移概率的矩阵，$A$​是观测状态生成概率的矩阵， $\pi$​是隐藏状态的初始概率分布。

同时我们也已经得到了观测序列$O=\{O_1,O_2,...O_T\}$​,现在我们要求观测序列$O$​在模型$\lambda$​下出现的条件概率$P(O|λ)$​。

乍一看，这个问题很简单。因为我们知道所有的隐藏状态之间的转移概率和所有从隐藏状态到观测状态生成概率，那么我们是可以暴力求解的。

概率问题，比较笨的办法，就是暴力求解

我们可以列举出所有可能出现的长度为$T$​​的隐藏序列$S=\{S_1,S_2,...,S_T\}$​​,分布求出这些隐藏序列与观测序列$O=\{O_1,O_2,...O_T\}$​​的联合概率分布$P(O,I|λ)$​​，这样我们就可以很容易的求出边缘分布$P(O|λ)$​​了。

具体暴力求解的方法是这样的：首先，任意一个隐藏序列$S=\{S_1,S_2,...,S_T\}$,出现的概率是：

$$P(S|\lambda)=\pi_{S_1}a_{S_1S_2}a_{S_2S_3}...a_{S_{T−1}S_T}$$

对于固定的状态序列$S=\{S_1,S_2,...,S_T\}$，我们要求的观察序列$O=\{O_1,O_2,...O_T\}$出现的概率是：

$$P(O|S,λ)=b_{S_1}(O_1)b_{S_2}(O_2)...b_{S_T}(O_T)$$

则$O$和$S$​​联合出现的概率是：

$$P(O,S|λ)=P(S|λ)P(O|S,λ)=\pi_{S_1}b_{S_1}(O_1)a_{S_1S_2}b_{S_2}(O_2)...a_{S_{T−1}S_T}b_{S_T}(O_T)$$

然后求边缘概率分布，即可得到观测序列O在模型$\lambda$下出现的条件概率$P(O|λ)$：

$$P(O|\lambda)=\sum_S P(O,S|\lambda )=\sum _{S_1,S_2,...S_T}\pi_{S_1}b_{S_1}(O_1)a_{S_1S_2}b_{S_2}(O_2)...a_{S_{T−1}S_T}b_{S_T}(O_T)$$

虽然上述方法有效，但是如果我们的隐藏状态数$N$​非常多的那就麻烦了，此时我们预测状态有$N^T$​种组合，算法的时间复杂度是$O(TN^T)$​阶的。因此对于一些隐藏状态数极少的模型，我们可以用暴力求解法来得到观测序列出现的概率，但是如果隐藏状态多，则上述算法太耗时，我们需要寻找其他简洁的算法。

上面的暴力求解太慢了，使用比较聪明的算法，向前向后算法

a) 前向算法

前向后向算法是前向算法和后向算法的统称，这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。

在给定模型的参数和观察序列$O=\{O_1,O_2,...O_T\}$,$\alpha_t(i)$表示$t$时刻$\alpha_t=i$的向前概率(从$t=1$时刻到$t$时刻观察序列$O=\{O_1,O_2,...O_T\}，\alpha_t=i$

$$\alpha_t(i)=P(O_1,O_2,\cdots,O_t,S_t=q_i|\lambda)$$

由前向递推关系$\alpha_t(i)$等于在所有可能的前一状态转移到当前状态（同时t时刻发射出观测值$O_t$)的概率之和：

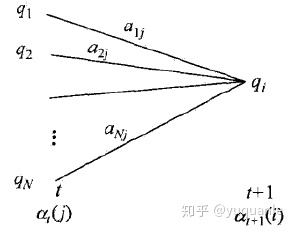
因此前向算法计算如下：

• 初值

  $\alpha_1(i)=\pi_{i1}b_{S_i}(O_1)$​

• 向前推进

  $\alpha_{t+1}(i)=[\sum_{j=1}^n\alpha_t(j)a_{ji}]b_{S_i}(O_{t+1})$

• 求和

  $P(O|\lambda)=\sum_{i=1}^n\alpha_T(i)$

b) 后向算法

在给定模型的参数和观察序列$O=\{O_{t+1},O_{t+2}，\cdots,O_T\}$下，$\beta_t(i)$表示$t$时刻$\alpha_t=i$的后向概率(从t时刻到T时刻观察序列$O=\{O_{t+1},O_{t+2}，\cdots,O_T\},\alpha_t=i$

$$\beta_t(i)=P(O_{t+1},O_{t+2},\cdots,O_T,S_t=q_i|\lambda)$$

值得注意的是，后向概率表示序列从t时刻到T时刻的概率,所以$\beta_t(i)\le \beta_{t+1}(j)$

由后向递推关系$\beta_t(i)$​等于所有可能的后一状态逆转移到当前状态（同时t+1时刻发射出观测值$O_{t+1}$)的概率之和

因此后向算法计算如下：

• 初值

  $\beta_T(i)=1,i=1,2,...n$

• 反向递推

  $\beta_t(i)=\sum_{j=1}^na_{ij}b_{S_j}(O_{t+1})\beta_{t+1}(j)$

• 求和

  $P(O|\lambda)=\sum_{i=1}^n\pi_{i1}b_{S_i}(O_1)\beta_1(i)$

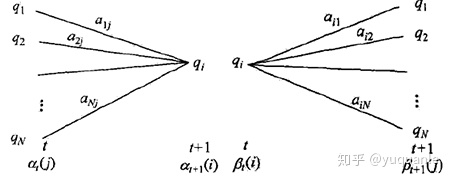
由上面的前向后向算法，固定t时刻的状态$S_t=q_i$，由前向后向算法有：

$$P(O|\lambda)=\sum_{i=1}^n\sum_{j=1}^n\alpha_t(i)a_{ij}b_{S_j}(O_{t+1})\beta_{t+1}(j),t=1,\cdots,T$$

2) 参数估计

转移概率$a_{ij}$表示从状态i转移到状态j的概率

$$a_{ij}=\frac{A_{ij}}{\sum_{j=1}^nA_{ij}},i=1,\cdots,n,j=1,\cdots,n$$

分子表示从i状态转移到j状态的次数

分母表示从i状态转到到任意状态的次数

发射概率$b_{S_j}(O_k)$表示在状态i下发射出观测值$O_k$的概率

$$b_{S_j}(O_k)=\frac{B_{ik}}{\sum_{k=1}^mB_{ik}} \\ i=1,\cdots,n,k \\ k=1,\cdots,m$$

其中分子表示在状态i下发射出观测值$O_k$的次数

分母表示在状态i下发射出任意状态的次数

初始状态转移概率$\pi_{i1}$为样本中初始状态的概率

$$\pi_{i1}=\frac{a_i}{\sum_{i=1}^na_i}$$

分子表示初始状态是i的次数

分母表示所有初始状态出现的次数

无监督（Baum-Welch）：

隐马尔可夫模型中隐状态其实是一个隐变量，EM算法这类含有隐变量模型的通用求解算法，思路是初始化一个隐变量的概率分布，E步：期望最大化来更新样本的隐变量(值，概率)，M步：在隐变量确定的条件下更新隐变量的概率。

3) 状态预测

已知模型的参数$\lambda=(\pi, A, B)$和观察序列O,求解一条使得该观测序列概率最大的隐状态序列 。这样概率计算类似，只需要求最大的即可。

维特比算法：维特比算法是一种动态规划算法来求解概率最大路径，也是一种求解最优路径问题。

而最优路径中总存在这样一个特性：如果最优路径t时刻通过节点$S_t$​,那么最优路径中从结点$S_t$到最终节点$S_T$的部分路径是可能从$S_t$到$S_T$路径最优的(同时从$S_1$到$S_t$的各种路径也是最优的)

依据这一特性，我们可以从$t=1$开始递推计算时刻$t$下状态为$S$的各种路径的最大概率，直至时刻$t=T$状态为$S$的最大概率。同时在递推的过程中，我们用一个变量来计住到达最优路径的上一个结点的状态。这样我们就首先确定了$t=T$时刻的状态值$S$,然后，根据到达该状态的上一个结点状态来递推到$S_{T-1},\cdots,S_t,\cdots ,S_1$​。

因此，我们需要引入两个变量，从$t=1$​时刻到$t$​时刻状态$S_i$​的最优路径的概率值，并以此来递推下一时刻状态为$S_i$​​的最优路径，即

$$\sigma_t(i)=\max_{S_1,S_2,\cdots.S_{t-1}}P(S_t=i,S_{t-1},\cdots,S_1,O_t,\cdots,O_1|\lambda)，i=1,2,\cdots,n \\ \sigma_{t+1}(i)=\max_{S_1,S_2,\cdots.S_{t}}P(S_{t+1}=i,S_{t},\cdots,S_1,O_{t+1},\cdots,O_1|\lambda)，i=1,2,\cdots,n,t=1,\cdots,T-1 \\ =\max_{j\in 1,\cdots,n}\sigma_t(j)a_{ji}b_{S_i}(O_{t+1})$$

同时为了记住到达该路径的上一节点的状态，定义如下变量：

$$\phi_t(i)=\arg \max_{j\in 1,\cdots,n}\sigma_{t-1}(j)a_{ji},i=1,\cdots,n$$

有了上面的两个变量，我们就可以获得隐状态的最优路径

• 初始化

  $\sigma_1(i)=\pi_{i1}b_{S_i}(O_1),i=1,\cdots,n$

  $\phi_1(i)=0$

• 递推，对$t=2,3,\cdots,T$

  $\sigma_t(i)=\max_{j\in 1,\cdots,n}\sigma_{t-1}(j)a_{ji}b_{S_i}(O_t),i=1,\cdots,n$

  $\phi_t(i)=\arg\max_{j\in 1,\cdots,n}\sigma_{t-1}(j)a_{ji},i=1,\cdots,n$

• 终止

  $P^*=\max_{i\in 1,\cdots,n}\sigma_T(i)$

  $i^*_T=\arg\max_{i\in 1,\cdots,n}\sigma_T(i)$

• 最优路径回溯，$t=T-1,\cdots,1$

  $i_t^*=\phi_{t+1}(i^*_t)$

求最优路径$I=\{i_1^*,i_2^*,\cdots,i_T^*\}$

其中值得注意的是，$\phi_1(i)=0$是无用的，在前向递推到$T$时刻获得最大概率的同时也获得了最优的最终状态$i^*_T$,回溯的过程只需要从$T-1$开始，不需要任何计算，因为$\phi$保存了到达当前最优路径状态的上一状态。

11.1.3 例子

假设有一个已知的HMM模型：

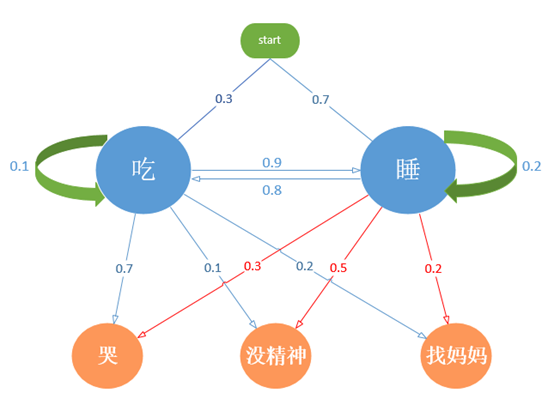
在该模型中，初始化概率$\pi=\{S_{吃}=0.3,S_{睡}=0.7\}$​；隐藏状态N=2；可观测状态M=3；转移矩阵和混淆矩阵分别是：

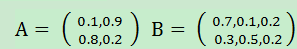
遍历法，最笨的方法

遍历法也是典型的穷举法，实现较为简单，罗列可能情况后将其相加即可。共有3种可观察状态，每个可观察状态对应2种隐藏状态，共有$2^3 = 8$中可能的情况。其中一种：

$$P(S_{吃1}, S_{吃2}, S_{吃3},O_{哭1},O_{累2},O_{累3}) \\ = P(S_{吃1})·P(O_{哭1})·P(S_{吃2})·P(O_{累2})·P(S_{吃3})·P(O_{累3}) \\ = (0.3×0.7)×(0.1×0.1)×(0.1×0.2) \\= 0.000042$$

上式中的下标的数字表示时间，下标在观测点和隐藏点都比较少的时候，遍历法最为有效（因为简单），一旦节点数增加，计算量将急剧增大。

1) 向前算法

向前算法是在时间$t=1$的时候，一步一步往前计算。

其背后的马尔可夫概率公式：

$$P(W_1,W_2) = P(W_1)P(W_2|W_1) \\ P(W_1,W_2,W_3) = P(W_1,W_2)P(W_3|W_1,W_2) \\ P(W_1,W_2,…,W_n) = P(W_1,W_2,…,W_{n-1})P(W_n|W_1,W_2,…,W_{n-1})$$

1.计算当$t=1$​时，发生$O_{哭}$​​这一行为的概率：

$$P(O_{哭},S_{吃}) = P(S_{吃})P(O_{哭}|S_{吃}) =0.3×0.7=0.21 \\ P(O_{哭},S_{睡}) = P(S_{睡})P(O_{哭}|S_{睡}) =0.7×0.3=0.21$$

2.计算当$t=2$​时，发生累这一行为的概率：

根据马尔可夫假设，$P(O_{t=2})$​仅与$S_{t=1}$​有关，下一天的行为概率是由前一天的状态计算而来，

如果$S_{t=2}=S_{吃2}$​：

$$P(O_{哭1},O_{累2},S_{吃2}) \\ = P(O_{哭1},S_{吃1})P(S_{吃2}|S_{吃1})P(O_{累2}|S_{吃2})+ P(O_{哭1},S_{睡1})P(S_{吃2}|S_{睡1})P(O_{累2}|S_{吃2}) \\ =[P(O_{哭1},S_{吃1})P(S_{吃2}|S_{吃1})+P(O_{哭1},S_{睡1})P(S_{吃2}|S_{睡1})]·P(O_{累2}|S_{吃2}) \\ = [0.21×0.1+0.21×0.8]×0.1 \\ = 0.0189$$

如果$S_{t=2}=S_{睡2}$：

$$P(O_{哭1},O_{累2},S_{睡2}) \\ = P(O_{哭1},S_{吃1})P(S_{睡2}|S_{吃1})P(O_{累2}|S_{睡2})+P(O_{哭1},S_{睡1})P(S_{睡2}|S_{睡1})P(O_{累2}|S_{睡2}) \\ = [P(O_{哭1},S_{吃1})P(S_{睡2}|S_{吃1})+ P(O_{哭1},S_{吃1})P(S_{睡2}|S_{吃1})]·P(O_{累2}|S_{睡2}) \\ = [0.21×0.9+0.21×0.2]×0.5 \\ = 0.1155$$

3.计算当$t=3$​时，发生Find这一行为的概率：

如果$S_{t=3}=S_{吃3}$，

$$P(O_{哭1},O_{累2},O_{找妈妈3},S_{吃3}) \\ = P(O_{哭1},O_{累2},S_{吃2})P(S_{吃3}| S_{吃2})P(O_{找妈妈3}|S_{吃3})+P(O_{哭1},O_{累2},S_{睡2})P(S_{吃3}| S_{睡2})P(O_{找妈妈3}|S_{吃3}) \\ = [P(O_{哭1},O_{累2},S_{吃2})P(S_{吃3}| S_{吃2})+P(O_{哭1},O_{累2},S_{睡2})P(S_{吃3}| S_{睡2})]·P(O_{找妈妈3}|S_{吃3}) \\ = [0.0189×0.1+0.1155×0.8]×0.2 \\ =0.018858$$

如果$S_{t=3}=S_{睡3}$，

$$P(O_{哭1},O_{累2},O_{找妈妈3},S_{吃3}) \\ = P(O_{哭1},O_{累2},S_{吃2})P(S_{睡3}| S_{吃2})P(O_{找妈妈3}|S_{睡3})+P(O_{哭1},O_{累2},S_{睡2})P(S_{睡3}| S_{睡2})P(O_{找妈妈3}|S_{睡3}) \\ = [P(O_{哭1},O_{累2},S_{吃2})P(S_{睡3}| S_{吃2})+P(O_{哭1},O_{累2},S_{睡2})P(S_{睡3}| S_{睡2})]·P(O_{找妈妈3}|S_{睡3}) \\ = [0.0189×0.9+0.1155×0.2]×0.2 \\ = 0.008022$$

综上，

$$P(O_{哭1},O_{累2},O_{找妈妈3}) \\ = P(O_{哭1},O_{累2},O_{找妈妈3},S_{吃3})+ P(O_{哭1},O_{累2},O_{找妈妈3},S_{睡3}) \\ = 0.018858+0.049602 \\ = 0.06848$$

2) 鲍姆-韦尔奇算法

3) 维特比算法

维特比算法的基础可以概括成下面三点：

• 如果概率最大的路径p(或者说最短路径)经过某个点，比如途中的$X_{22}$​，那么这条路径上的起始点S到$X_{22}$​的这段子路径Q，一定是S到$X_{22}$​之间的最短路径。
• 否则，用S到$X_{22}$​的最短路径R替代Q，便构成一条比P更短的路径，这显然是矛盾的。证明了满足最优性原理。
• 从S到E的路径必定经过第i个时刻的某个状态，假定第i个时刻有k个状态，那么如果记录了从S到第i个状态的所有k个节点的最短路径，最终的最短路径必经过其中一条，这样，在任意时刻，只要考虑非常有限的最短路即可。
• 结合以上两点，假定当我们从状态i进入状态i+1时，从S到状态i上各个节的最短路径已经找到，并且记录在这些节点上，那么在计算从起点S到第i+1状态的某个节点$X_{i+1}$​的最短路径时，只要考虑从S到前一个状态i所有的k个节点的最短路径，以及从这个节点到$X_{i+1}$​，j的距离即可。

在本例中，维特比算法实际上是从$t=1$时刻开始，不断向后计算，寻找概率最大的路径。

1.计算$t=1$时刻$O_{哭}$​发生的概率：

$$\delta 11 = P(O_{哭},S_{吃}) = P(S_{吃})P(O_{哭}|S_{吃})=0.3×0.7=0.21 \\ \delta 12 = P(O_{哭},S_{睡}) = P(S_{睡})P(O_{哭}|S_{睡})=0.7×0.3=0.21$$

2.计算t=2时刻$O_{累}$​发生的概率：

$$\delta 21 =max(P(O_{哭1},S_{吃1})P(S_{吃2}|S_{吃1})P(O_{累2}|S_{吃2}),P(O_{哭1},S_{睡1})P(S_{吃2}|S_{睡1})P(O_{累2}|S_{吃2})) \\ = max(P(O_{哭1},S_{吃1})P(S_{吃2}|S_{吃1}), P(O_{哭1},S_{睡1})P(S_{吃2}|S_{睡1}))·P(O_{累2}|S_{吃2}) \\ = max(δ11 P(S_{吃2}|S_{吃1}), δ12 P(S_{吃2}|S_{睡1})) ·P(O_{累2}|S_{吃2}) \\ = max(0.21×0.1,0.21×0.8)×0.1 \\ = 0.0168 \\ S_{21} = 吃 \\ \delta 22 = max(P(O_{哭1},S_{吃1})P(S_{吃2}|S_{吃1})P(O_{累2}|S_{睡2}),P(O_{哭1},S_{睡1})P(S_{吃2}|S_{睡1})P(O_{累2}|S_{睡2})) \\ = max(δ11 P(S_{睡2}|S_{吃1}), δ12 P(S_{睡2}|S_{睡1})) ·P(O_{累2}|S_{睡2}) \\ = max(0.21×0.9,0.21×0.2)×0.5 \\ = 0.0945 \\ S_{22} = 睡$$

3.计算t=3时刻$O_{找妈妈}$​发生的概率：

$$\\ \delta_{31} = max(\delta_{21}P(S_{吃3}|S_{吃2}), \delta_{22}P(S_{吃3}|S_{睡2})) ·P(O_{找妈妈3}|S_{吃3}) \\ =max(0.0168×0.1, 0.0189×0.8)×0.2 \\ =0.003024 \\ S_{31} = 吃 \\ \delta32 = max(δ21P(S_{睡3}|S_{吃2}), \delta_{22}P(S_{睡3}|S_{睡2})) ·P(O_{找妈妈3}|S_{睡3}) \\ =max(0.0168×0.9, 0.0189×0.2)×0.2 \\ =0.003024 \\ S_{31} = 睡$$

4.回溯，每一步的最大概率：

$$max(\delta_{11},\delta_{12}), max(\delta_{21},\delta2_{22}), max(\delta_{31},\delta_{32})$$

对应的状态：吃 or 睡, 睡, 吃 or 睡

11.2 马尔可夫随机场

参考资料

https://www.cnblogs.com/jiangxinyang/p/9309742.html

参考资料2

https://zhuanlan.zhihu.com/p/112980214

马尔科夫随机场是典型的马尔科夫网（MRF），是一个可以由无向图表示的概率分布模型。图中每个结点表示一个或者一组变量，结点之间的边表示两个变量之间的依赖关系。在马尔科夫随机场中存在一组势函数（定义在变量子集上的非负实函数），也称为因子，主要是用于定义概率分布函数。

11.3 条件随机场