GRU

1. 简介

序列信号中，可能存在跨度很大的词性依赖关系。例如下面这个例子∶

The ==child==, which already ate candy, ==was== happy. The ==children==,which already ate candy, ==were== happy.

第一句话中，was 受child影响;第二句话中，were 受 children 影响，它们之间的间隔较远。

一般的RNN模型中，每个元素受其周围附近的影响较大，难以建立跨度较大的依赖性。

上面两句话的这种依赖关系，由于跨度很大，普通的RNN模型就容易出现梯度消失，捕捉不到它们之间的依赖，造成语法错误。关于梯度消失和梯度爆炸我们在之前介绍神经网络的时候已经介绍过了，此处不再赘述。

解决的问题

RNN处理不了太长的序列，因为RNN把所有的数据放进了隐藏状态里面，到后面的时候呢，那个隐藏状态就累积了太多的东西，会前面的信息就提取不出来了

GRU（Gate Recurrent Unit）是循环神经网络（Recurrent Neural Network, RNN）的一种。和LSTM（Long-Short Term Memory）一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。

GRU和LSTM在很多情况下实际表现上相差无几，那么为什么我们要使用新人GRU（2014年提出）而不是相对经受了更多考验的LSTM（1997提出）呢。

为啥先将GRU？？？因为比较简单。

2. 架构讲解

首先看一下一副图片，图片中有很多猫，突然来了一只猫，我们自然而然的会关注这只老师，其他的猫会被忽略

在GRU中如何实现这样子的功能呢？

只记住相关的观察需要的东西

• 能关注的机制(更新门)
• 能遗忘的机制(重置门)，到目前为止，我觉得这个东西不重要

2.1 门控隐状态

门控循环单元与普通的循环神经⽹络之间的关键区别在于：

后者⽀持隐状态的门控。这意味着模型有专⻔的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。

这些机制是可学习的，并且能够解决了上⾯列出的问题。

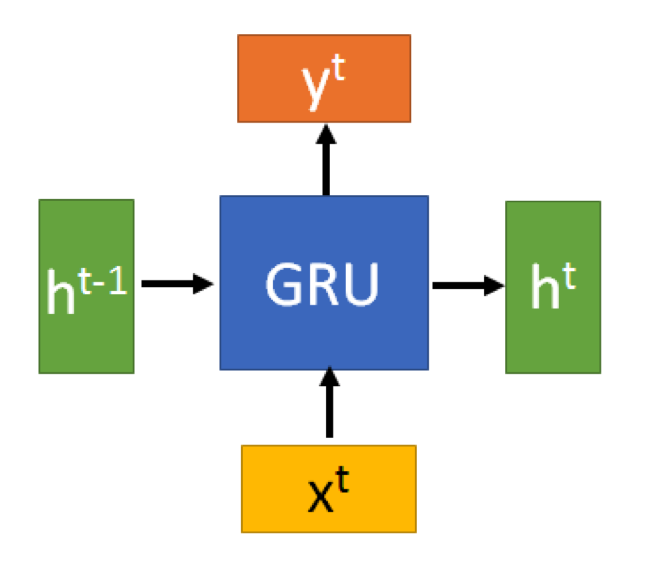
GRU的输入输出结构与普通的RNN是一样的

有一个当前的输入$x^t$，和上一个节点传递下来的隐状态$h^{t-1}$,这个隐状态包含了之前节点的相关信息

结合$x^t$和$h^{t-1}$,GRU会得到当前隐藏节点的输出$y^t$和传递给下一个节点的隐状态$h^t$

2.1.1 重置门和更新门

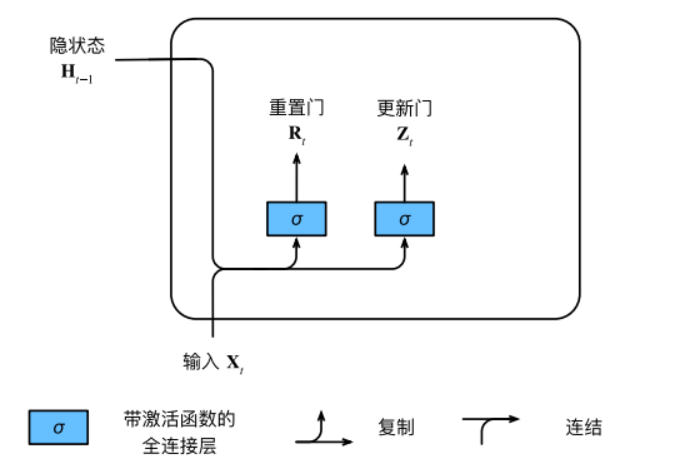
我们⾸先介绍重置门（reset gate）和更新门（update gate）。

更新门

更新门帮助模型决定到底要将多少过去的信息传递到未来，或到底前一时间步和当前时间步的信息有多少是需要继续传递的。

这一点非常强大，因为模型能决定从过去复制所有的信息以减少梯度消失的风险。

我们随后会讨论更新门的使用方法，现在只需要记住 $Z_t$ 的计算公式就行。

重置门

本质上来说，重置门主要决定了到底有多少过去的信息需要遗忘

计算公式如下

$$R_t=\sigma(X_tW_{xr}+H_{t-1}W_{hr}+b_r) \\ Z_t=\sigma(X_tW_{xz}+H_{t-1}W_{hz}+b_z)$$

其中$\sigma$为$sigma$的函数，$X_t$输入，$W_{xr}$就是权重信息

我们把它们设计成$(0,1)$区间中的向量，这样我们就可以进⾏凸组合。

Sigmoid 层输出0到 1之间的数值，描述每个部分有多少量可以通过。

0 代表“不许任何量通过”，1 就指“允许任意量通过”

2.1.2 候选隐状态

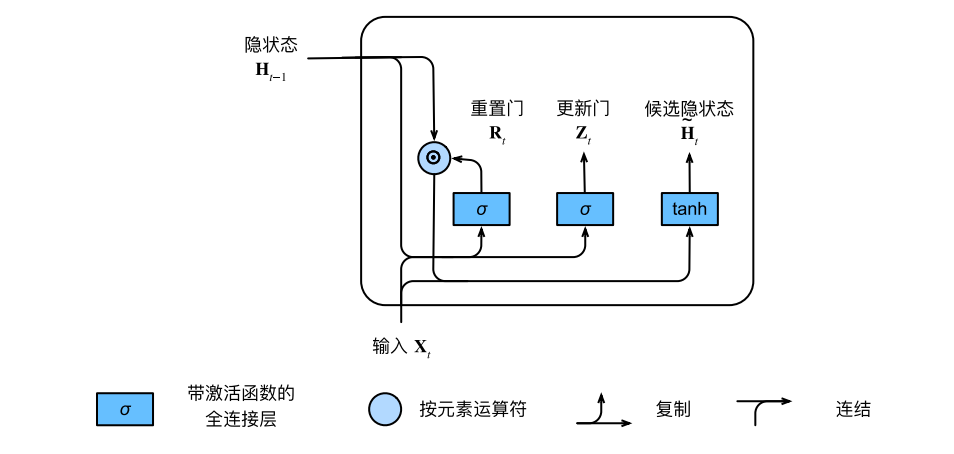
首先我们将重置门和常规隐状态更新机制集成，得到在时间步$t$候选隐状态$\hat{H_t}$

$$\hat{H_t}=tanh(X_tW_{xh}+(R_t \odot H_{t-1})W_{hh}+b_h)$$

$R_t \odot H_{t-1}$是啥意思呢？？假设$R_t$靠近零，$R_t \odot H_{t-1}$就会变的向零，意思为把上一个隐藏状态给忘记

另一种极端状态$R_t$都是1,意味着全部的隐藏层状态都拿过来，就等价于RNN实现的东西。保留了当前状态信息$X_t$和上一个隐藏状态的全部关系

计算$R_t$的权重可以进行学习，学习那些东西可以丢弃，那些东西必须保留

候选隐状态$\hat{H_t}$其实就是当前记忆内容。

在重置门的使用中，新的记忆内容将使用重置门储存过去相关的信息。

通过重置门，决定有多少过去的隐状态信息被保留。

2.1.3 最后一步-隐状态

上面呢？？我们只是结合了重置门，现在呢，还需要再加上更新门$Z_t$。就能做到效果了。

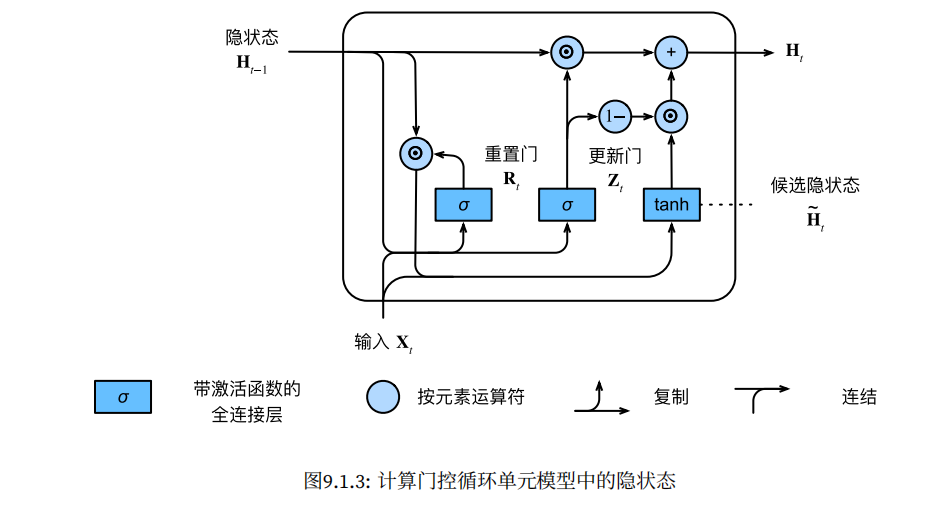
在最后一步，网络需要计算 $H_t$，该向量将保留当前单元的信息并传递到下一个单元中.到底是输出多少的当前信息隐状态$\hat{H}_{t}$，还有多少的过去状态信息$H_{t-1}$

这一步确定了新的隐状态$H_t$在很大程序上只需要来自旧的状态$H_{t-1}$和新的候选状态$\hat{H_t}$.更新门$Z_t$仅需要在$H_{t-1}$和$\hat{H_t}$进行按照元素的凸组合就可以实现这个目标。更新公式为

$$H_T=Z_t\odot H_{t-1}+(1-Z_t)\odot \hat{H_t}$$

当更新门$Z_t$接近1时，模型就倾向只保留旧状态，此时新的输入$X_t$就会被忽略，

相反，当$Z_t$接近0时，新的隐藏状态$H_t$就会接近候选隐状态$\hat{H_t}$.

这样子就会更好的捕捉距离很长的序列的依赖关系

2.2 流程

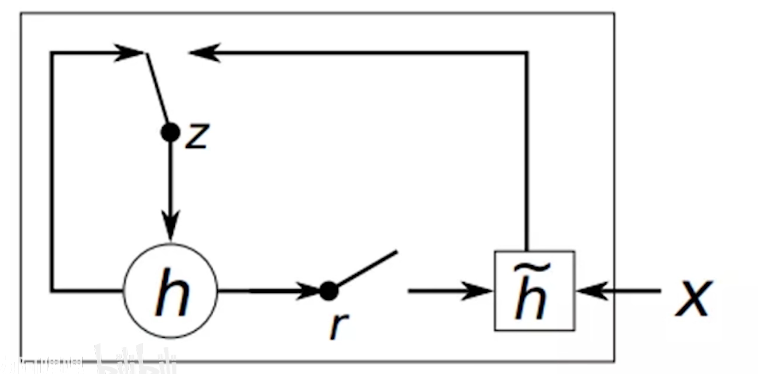
2.3 小结

总之，门控循环单元具有以下两个显著特征:

• 重置门有助于捕获序列中的短期依赖关系。

• 更新门有助于捕获序列中的长期依赖关系。

3. 代码讲解

(2条消息) RNN学习笔记（六）-GRU，LSTM 代码实现_rtygbwwwerr的博客-CSDN博客_gru代码 (opens new window)

初始化参数

def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    W_xz, W_hz, b_z = three()  # 更新门参数
    W_xr, W_hr, b_r = three()  # 重置门参数
    W_xh, W_hh, b_h = three()  # 候选隐状态参数
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

定义模型

现在我们将定义隐状态的初始化函数init_gru_state。

def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

现在我们准备定义门控循环单元模型， 模型的架构与基本的循环神经网络单元是相同的， 只是权重更新公式更为复杂。

def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)