4.4 nn.BatchNorm2d用法详解

简介

BatchNorm2d()函数数学原理如下：

$$y=\frac{x-E(x)}{\sqrt{Var[x]+\varepsilon}}*\gamma+\beta$$

代码

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, 
						track_running_stats=True, device=None, dtype=None)

参数详解

• num_features:指特征数。 一般情况下输入的数据格式为（batch_size ，num_features ， height ， width）其中的C为特征数，也称channel数
• eps:为分数值稳定而添加到分母的值。 默认值：1e-5
• momentum:一个用于运行过程中均值和方差的一个估计参数。 可以将累积移动平均线（即简单平均线）设置为 None 。 默认值：0.1
• affine:一个布尔值，当设置为True时，此模块具有可学习的仿射参数。γ(gamma) 和 β(beta) （可学习的仿射变换参数） 默认值：True
• track_running_stats:一个布尔值，当设置为True时，此模块跟踪运行平均值和方差；设置为False时，此模块不跟踪此类统计信息，并将统计信息缓冲区running_mean和running_var初始化为None。 当这些缓冲区为None时，此模块将始终使用批处理统计信息。 在训练和评估模式下都可以。 默认值：True

作用

机器学习中，进行模型训练之前，需对数据做归一化处理，使其分布一致。在深度神经网络训练过程中，通常一次训练是一个batch，而非全体数据。每个batch具有不同的分布产生了internal covarivate shift问题——在训练过程中，数据分布会发生变化，对下一层网络的学习带来困难。Batch Normalization强行将数据拉回到均值为0，方差为1的正太分布上，一方面使得数据分布一致，另一方面避免梯度消失。

运算

说明Batch Normalization的原理。假设在网络中间经过某些卷积操作之后的输出的feature maps的尺寸为N×C×W×H，5为batch size（N），3为channel（C），W×H为feature map的宽高，则Batch Normalization的计算过程如下：

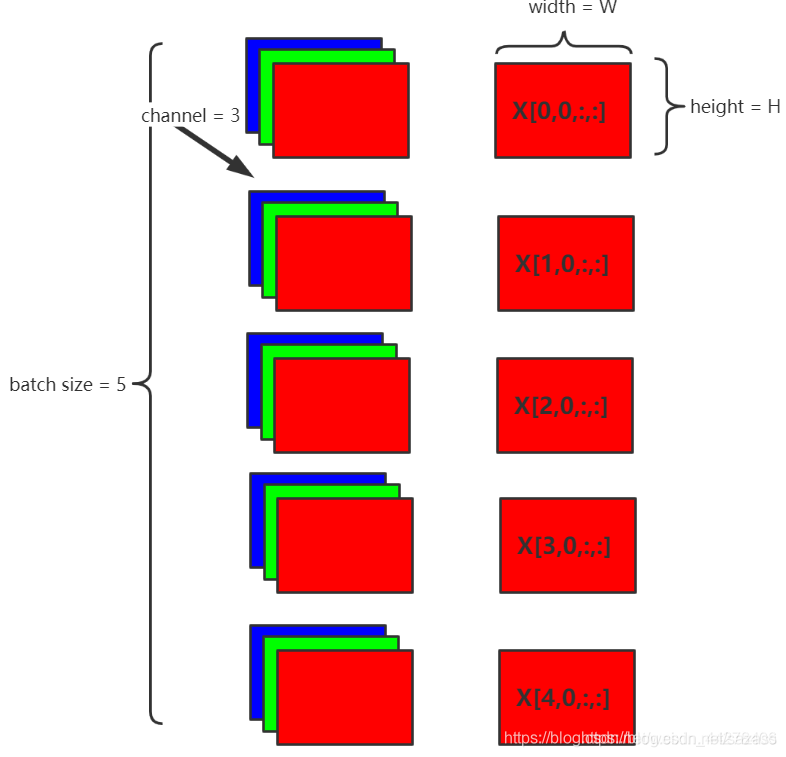
1. 每个batch计算同一通道的均值$\mu$，如图取channel 0，即$c=0$（红色表示）

   $$\mu=\frac{\sum_{n=0}^{N-1}\sum_{w=0}^{W-1}\sum_{h=0}^{H-1}X[n,c,w,h]}{N\times W\times H}$$

2. 每个batch计算同一通道的方差$\sigma^2$

   $$\sigma^2=\frac{\sum_{n=0}^{N-1}\sum_{w=0}^{W-1}\sum_{h=0}^{H-1}(X[n,c,w,h]-\mu)^2}{N\times W\times H}$$

3. 对当前channel下feature map中每个点$x$，索引形式$X[n, c, w, h]$，做归一化

   $$x^\prime=\frac{(x-\mu)}{\sqrt{\sigma^2+\varepsilon}}$$

4. 增加缩放和平移变量 γ 和 β （可学习的仿射变换参数），归一化后的值

   $$y=\gamma x^\prime +\beta$$

5. 简化公式

   $$y=\frac{x-\mu}{\sqrt{\sigma^2+\varepsilon}}\gamma +\beta$$

代码

import torch
import torch.nn as nn

def checkBN(debug = False):
    # parameters
    N = 5 # batch size
    C = 3 # channel
    W = 2 # width of feature map
    H = 2 # height of feature map
    # batch normalization layer
    BN = nn.BatchNorm2d(C,affine=True) #gamma和beta, 其维度与channel数相同
    # input and output
    featuremaps = torch.randn(N,C,W,H)
    output = BN(featuremaps)
    # checkout
    ###########################################
    if debug:
        print("input feature maps：\n",featuremaps)
        print("normalized feature maps: \n",output)
    ###########################################
    
    # manually operation, the first channel
    X = featuremaps[:,0,:,:]
    firstDimenMean = torch.Tensor.mean(X)
    firstDimenVar = torch.Tensor.var(X,False) #Bessel's Correction贝塞尔校正不被使用
    
    BN_one = ((input[0,0,0,0] - firstDimenMean)/(torch.pow(firstDimenVar+BN.eps,0.5) )) * BN.weight[0] + BN.bias[0]
    print('+++'*15,'\n','manually operation: ', BN_one)
    print('==='*15,'\n','pytorch result: ', output[0,0,0,0])
    
if __name__=="__main__":
    checkBN()

可以看出手算的结果和PyTorch的nn.BatchNorm2d的计算结果一致：

+++++++++++++++++++++++++++++++++++++++++++++
 manually operation:  tensor(-0.0327, grad_fn=<AddBackward0>)
=============================================
 pytorch result:  tensor(-0.0327, grad_fn=<SelectBackward>)

官方演示代码

>>> # With Learnable Parameters
>>> m = nn.BatchNorm2d(100)
>>> # Without Learnable Parameters
>>> m = nn.BatchNorm2d(100, affine=False)
>>> input = torch.randn(20, 100, 35, 45)
>>> output = m(input)