飞哥的技术博客
Source (opens new window)

4.2 池化层讲解

joker ... 2022-4-7 大约 9 分钟

# 4.2 池化层讲解

# 1. 简介

# 1.1 简介

比卷积的计算方法还要简单。以二维最大池化层为例，池化窗口从输入数组的最左上方开始，从左到右，从上到下，依次在输入数组上滑动。当池化窗口滑动到某一位置时，窗口中的输入子数组的最大值即输入数组中相应位置的元素。很绕是吧，看文字我也晕。

img

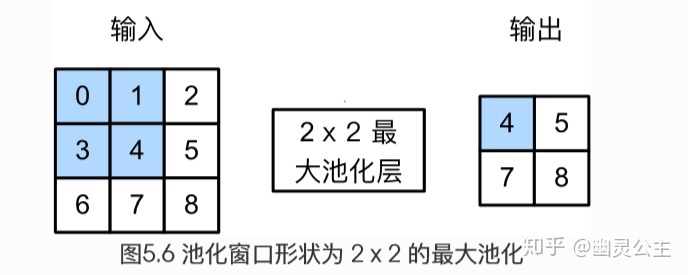
# 1.2 意义

池化它有啥作用呢？

魏秀参博士在CNN_book一书中做了很好的解答：

  1. 特征不变性（feature invariant） 汇合操作使模型更关注是否存在某些特征而不是特征具体的位置 可看作是一种很强的先验，使特征学习包含某种程度自由度，能容忍一些特征微小的位移
  2. 特征降维 由于汇合操作的降采样作用，汇合结果中的一个元素对应于原输入数据的一个子区域（sub-region），因此汇合相当于在空间范围内做了维度约减（spatially dimension reduction），从而使模型可以抽取更广范围的特征 同时减小了下一层输入大小，进而减小计算量和参数个数
  3. 在一定程度上能防止过拟合的发生

三种池化的意义

  1. 最大池化可以获取局部信息，可以更好保留纹理上的特征。如果不用观察物体在图片中的具体位置，只关心其是否出现，则使用最大池化效果比较好。
  2. 平均池化往往能保留整体数据的特征，能凸出背景的信息。
  3. 随机池化中元素值大的被选中的概率也大，但不是像最大池化总是取最大值。随机池化一方面最大化地保证了Max值的取值，一方面又确保了不会完全是max值起作用，造成过度失真。除此之外，其可以在一定程度上避免过拟合。

# 2. 池化公式

最大池化输出

Hout=Hin+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1stride[0]+1Wout=Win+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1stride[0]+1H_{out}=\frac{H_{in}+2\times padding[0] -dilation[0]\times(kernel\_size[0]-1)-1}{stride[0]}+1 \\ W_{out}=\frac{W_{in}+2\times padding[0] -dilation[0]\times(kernel\_size[0]-1)-1}{stride[0]}+1

下面我们写代码验证一下最大池化层是如何计算的：

# 3. 参数讲解

我们先来看一下基本参数，一共六个：

kernel_size：表示做最大池化的窗口大小，可以是单个值，也可以是tuple元组 stride ：步长，可以是单个值，也可以是tuple元组 padding ：填充，可以是单个值，也可以是tuple元组 dilation ：控制窗口中元素步幅 return_indices ：布尔类型，返回最大值位置索引 ceil_mode ：布尔类型，为True，用向上取整的方法，计算输出形状；默认是向下取整。

  • 关于 kernel_size 的详解：

    注意这里的kernel_size 跟卷积核不是一个东西。kernel_size 可以看做是一个滑动窗口，这个窗口的大小由自己指定，如果输入是单个值，例如 (3,3)(3,3) ，那么窗口的大小就是 3×33\times 3 ，还可以输入元组，例如$ (3, 2)$ ，那么窗口大小就是 3×33\times 3。

    最大池化的方法就是取这个窗口覆盖元素中的最大值。

  • 关于 stride 的详解：

    上一个参数我们确定了滑动窗口的大小，现在我们来确定这个窗口如何进行滑动。如果不指定这个参数，那么默认步长跟最大池化窗口大小一致。如果指定了参数，那么将按照我们指定的参数进行滑动。例如 stride=(2,3)stride=(2,3) ， 那么窗口将每次向右滑动三个元素位置，或者向下滑动两个元素位置。

  • 关于padding 的详解：

    这参数控制如何进行填充，填充值默认为0。如果是单个值，例如 1，那么将在周围填充一圈0。还可以用元组制定如何填充，例如padding=(2,1)padding=(2,1)，表示在上下两个方向个填充两行0，在左右两个方向各填充一列0。

  • 关于 dilation 的详解：

  • 关于 return_indices 的详解：

    这是个布尔类型值，表示返回值中是否包含最大值位置的索引。注意这个最大值指的是在所有窗口中产生的最大值，如果窗口产生的最大值总共有5个，就会有5个返回值。

  • 关于ceil_mode 的详解：

    这个也是布尔类型值，它决定的是在计算输出结果形状的时候，是使用向上取整还是向下取整。怎么计算输出形状，下面会讲到。一看就知道了。

首先验证 kernel_size 参数：

import torch
import torch.nn as nn

# 仅定义一个 3x3 的池化层窗口
m = nn.MaxPool2d(kernel_size=(3, 3))

# 定义输入
# 四个参数分别表示 (batch_size, C_in, H_in, W_in)
# 分别对应，批处理大小，输入通道数，图像高度（像素），图像宽度（像素）
# 为了简化表示，我们只模拟单张图片输入，单通道图片，图片大小是6x6
input = torch.randn(1, 1, 6, 6)

print(input)

output = m(input)

print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

第一个tensor是我们的输入数据 1×1×6×61\times 1 \times 6 \times 6，我们画红线的区域就是我们设置的窗口大小3×33 \times 3 ，背景色为红色的值，为该区域的最大值。

第二个tensor就是我们最大池化后的结果，跟我们标注的一模一样。

这个就是最基本的最大池化。

之后我们验证一下 stride 参数：

import torch
import torch.nn as nn

# 仅定义一个 3x3 的池化层窗口
m = nn.MaxPool2d(kernel_size=(3, 3), stride=(2, 2))

# 定义输入
# 四个参数分别表示 (batch_size, C_in, H_in, W_in)
# 分别对应，批处理大小，输入通道数，图像高度（像素），图像宽度（像素）
# 为了简化表示，我们只模拟单张图片输入，单通道图片，图片大小是6x6
input = torch.randn(1, 1, 6, 6)

print(input)

output = m(input)

print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

红色的还是我们的窗口，但是我们的步长变为了2，可以看到第一个窗口和向右滑动后的窗口，他们的最大值刚好是重叠的部分都是2.688，向下滑动之后，最大值是0.8030，再次向右滑动，最大值是2.4859。

可以看到我们在滑动的时候省略了部分数值，因为剩下的数据不够一次滑动了，于是我们将他们丢弃了。

其实最后图片的宽度和高度还可以通过上面两个公式来计算，我们公式中用的是向下取整，因此我们丢弃了不足的数据。现在我们试试向上取整。

利用 ceil_mode 参数向上取整

import torch
import torch.nn as nn

# 仅定义一个 3x3 的池化层窗口
m = nn.MaxPool2d(kernel_size=(3, 3), stride=(2, 2), ceil_mode=True)

# 定义输入
# 四个参数分别表示 (batch_size, C_in, H_in, W_in)
# 分别对应，批处理大小，输入通道数，图像高度（像素），图像宽度（像素）
# 为了简化表示，我们只模拟单张图片输入，单通道图片，图片大小是6x6
input = torch.randn(1, 1, 6, 6)

print(input)

output = m(input)

print('\n\n\n\n\n')

print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

从结果可以看出，输出的size由原来的2×22 \times 2变成了现在的3×33 \times 3。这就是向上取整的结果。为什么会出现这样的结果呢？

这看起来像是我们对输入进行了填充，但是这个填充值不会参与到计算最大值中。

继续验证 padding 参数：

import torch
import torch.nn as nn

# 仅定义一个 3x3 的池化层窗口
m = nn.MaxPool2d(kernel_size=(3, 3), stride=(3, 3), padding=(1, 1))

# 定义输入
# 四个参数分别表示 (batch_size, C_in, H_in, W_in)
# 分别对应，批处理大小，输入通道数，图像高度（像素），图像宽度（像素）
# 为了简化表示，我们只模拟单张图片输入，单通道图片，图片大小是6x6
input = torch.randn(1, 1, 6, 6)

print(input)

output = m(input)

print('\n\n')

print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

我们对周围填充了一圈0，我们滑动窗口的范围就变化了，这就是填充的作用。

但是有一点需要注意，就是即使我们填充了0，这个0也不会被选为最大值。例如上图的左上角四个数据，如果我们全部变为负数，结果是-0.1711，而不会是我们填充的0值，这一点要注意。

最后验证 return_indices 参数：

import torch
import torch.nn as nn

# 仅定义一个 3x3 的池化层窗口
m = nn.MaxPool2d(kernel_size=(3, 3), return_indices=True)

# 定义输入
# 四个参数分别表示 (batch_size, C_in, H_in, W_in)
# 分别对应，批处理大小，输入通道数，图像高度（像素），图像宽度（像素）
# 为了简化表示，我们只模拟单张图片输入，单通道图片，图片大小是6x6
input = torch.randn(1, 1, 6, 6)

print(input)

output = m(input)

print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

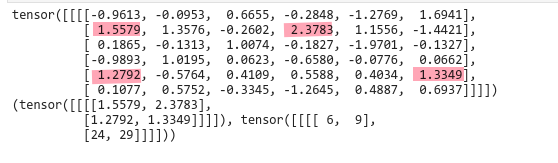
仅仅是多返回了一个位置信息。元素位置从0开始计数，6表示第7个元素，9表示第10个元素…需要注意的是，返回值实际上是多维的数据，但是我们只看相关的元素位置信息，忽略维度的问题。

# 4. 下采样

from PIL import Image
from matplotlib import pyplot as plt
import numpy as np
import torch.nn as nn
import torch

img = Image.open('./test.jpg')
img = np.array(img)
print("图片的尺寸", img.shape)

plt.imshow(img)
img = np.array(img).transpose(2, 0, 1)

m = nn.MaxPool2d(kernel_size=(3,3), stride=(2,2))
torch_img = torch.FloatTensor(img)
out = m(torch_img)
print(out.shape)

plt.figure()
mean_pool_img = out.transpose(0,2).transpose(0,1)
# 把图像变成
mean_pool_img = mean_pool_img.numpy().clip(0, 255).astype(int)
plt.imshow(mean_pool_img)
print("下采样后图片大小",mean_pool_img.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结果如下

图片的尺寸 (200, 200, 3)
torch.Size([3, 99, 99])
下采样后图片大小 (99, 99, 3)
1
2
3

下采样1/2后。图片的展示效果

image-20220405151534192

参考链接

https://blog.csdn.net/quiet_girl/article/details/84579038

4.3 上采样方法介绍

Copyright © 2021-present joker