4.1 CNN 卷积核与通道讲解
# 4.1 CNN 卷积核与通道讲解
具体讲解----https://blog.csdn.net/lyj223061/article/details/108709447
CNN在图像和提取空间信息中有着广泛应用,本篇博客以图像解释为主,省去了CNN基础内容的概述,主要讲述单通道卷积核多通道卷积的详细过程,并以Pytorch代码示例。
# 1. 函数讲解
# nn.Conv1d
cove1d:用于文本数据,只对宽度进行卷积,对高度不进行卷积 cove2d:用于图像数据,对宽度和高度都进行卷积
# nn.Conv2d
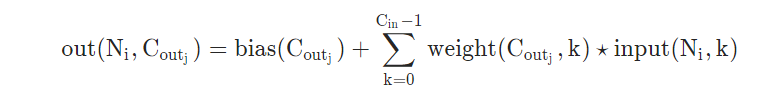

class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
参数讲解
卷积一层的几个参数:
in_channels=3:表示的是输入的通道数,RGB型的通道数是3.out_channels:表示的是输出的通道数,设定输出通道数(这个是可以根据自己的需要来设置的)kernel_size=12:表示卷积核的大小是12x12的,也就是上面的 F=12stride=4:表示的是步长为4,也就是上面的S=4padding=2:表示的是填充值的大小为2,也就是上面的P=2
注意:卷积核大小一般为奇数,原因如下:
①当卷积核为偶数时,p不为整数,假设是Same模式,若想使得卷积之后的维度和卷积之前的维度相同,则需要对图像进行不对称填充,较复杂。 ②当kernel为奇数维时,有中心像素点,便于定位卷积核。
# 2. 单通道卷积
以单通道卷积为例,输入为(1,5,5),分别表示1个通道,宽为5,高为5。假设卷积核大小为3x3,padding=0,stride=1。
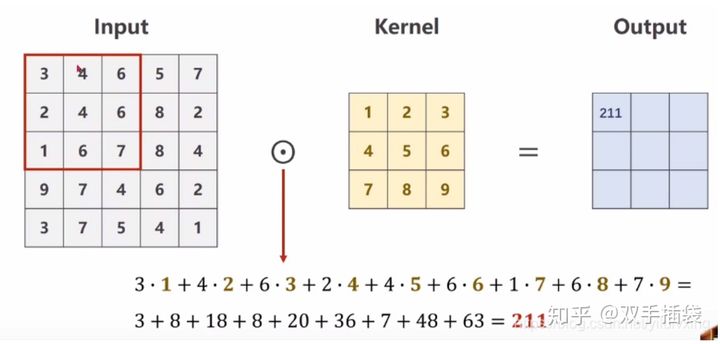
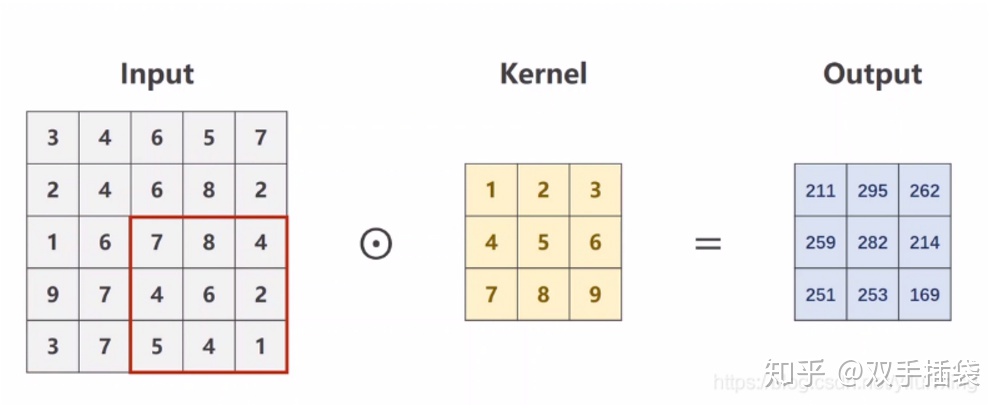
相应的卷积核不断的在图像上进行遍历,最后得到3x3的卷积结果,结果如下:
import numpy as np
import torch
m = np.array([[3, 4, 6, 5, 7],
[2, 4, 6, 8, 2],
[1, 6, 7, 8, 4],
[9, 7, 4, 6, 2],
[3, 7, 5, 4, 1]])
x = torch.tensor(m, dtype=torch.float).resize(1, 1, 5, 5)
# 一定要设置偏置为false,不然下面的计算就得手动添加
# 卷积核的内容,每次都是随机的
cov1 = torch.nn.Conv2d(in_channels=1,
out_channels=1,
kernel_size=(3, 3),
stride=(1, 1),
bias=False)
print("卷积后的数值", cov1(x))
# print("卷积核的参数", list(cov1.parameters()))
print("-----------检验一下是不是正确的-------------")
# 获取卷积核的Kernel内容的值
kernel = list(cov1.parameters())[0][0][0].detach().numpy()
# 卷积部分的第一个参数
temp = m[0:3, 0:3].astype(float)
print("卷积内容的第一个参数的值")
# 可能因为精度的问题,差距总在0.2 之间
print(np.multiply(temp, kernel).sum())
print("第一个3*3的卷积部分\n", temp)
print("卷积核的内容\n", kernel)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
结果如下
卷积后的数值 tensor([[[[-2.1805, -1.7721, -3.6701],
[-0.4743, -1.1107, -3.5471],
[-3.1629, -1.8610, -2.5680]]]], grad_fn=<SlowConv2DBackward0>)
-----------检验一下是不是正确的-------------
卷积内容的第一个参数的值
-2.1804784536361694
第一个3*3的卷积部分
[[3. 4. 6.]
[2. 4. 6.]
[1. 6. 7.]]
卷积核的内容
[[-0.222 0.019 -0.013]
[-0.134 -0.13 0.125]
[ 0.229 -0.3 0.015]]
2
3
4
5
6
7
8
9
10
11
12
13
14
# 2. 多通道卷积1
以彩色图像为例,包含三个通道,分别表示RGB三原色的像素值,输入为(3,5,5),分别表示3个通道,每个通道的宽为5,高为5。假设卷积核只有1个,卷积核通道为3,每个通道的卷积核大小仍为3x3,padding=0,stride=1。
卷积过程如下,每一个通道的像素值与对应的卷积核通道的数值进行卷积,因此每一个通道会对应一个输出卷积结果,三个卷积结果对应位置累加求和,得到最终的卷积结果(这里卷积输出结果通道只有1个,因为卷积核只有1个。卷积多输出通道下面会继续讲到)。
可以这么理解:最终得到的卷积结果是原始图像各个通道上的综合信息结果。
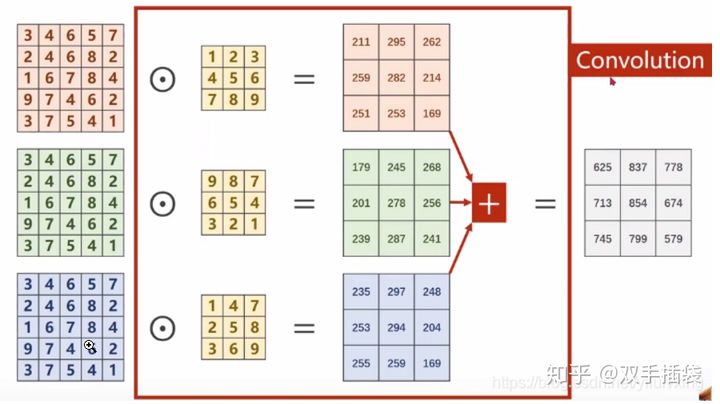
上述过程中,每一个卷积核的通道数量,必须要求与输入通道数量一致,因为要对每一个通道的像素值要进行卷积运算,所以每一个卷积核的通道数量必须要与输入通道数量保持一致
我们把上述图像通道如果放在一块,计算原理过程还是与上面一样,堆叠后的表示如下:
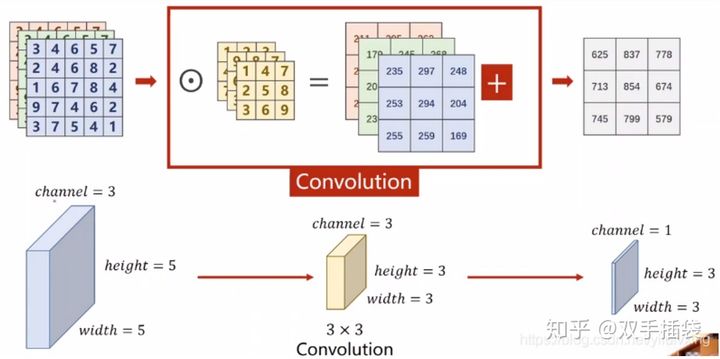
# 4. 多通道卷积2
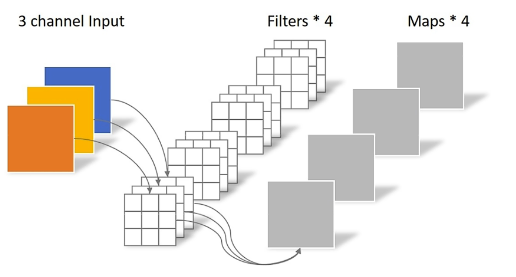
在上面的多通道卷积1中,输出的卷积结果只有1个通道,把整个卷积的整个过程抽象表示,过程如下:
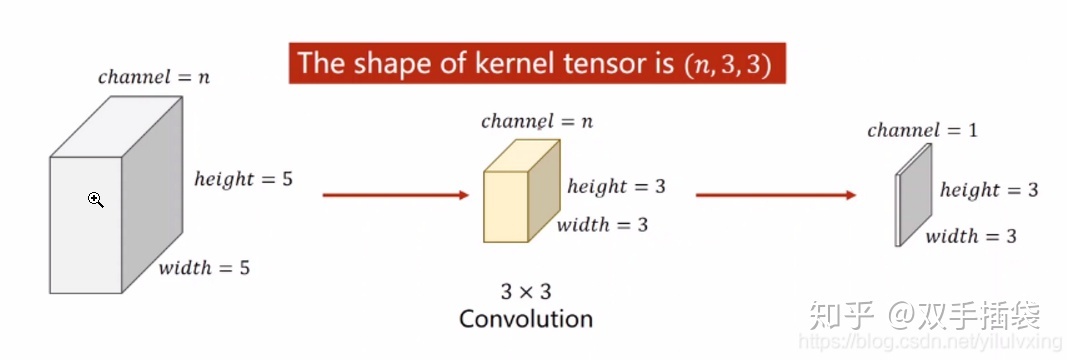
即:由于只有一个卷积核,因此卷积后只输出单通道的卷积结果(黄色的块状部分表示一个卷积核,黄色块状是由三个通道堆叠在一起表示的,每一个黄色通道与输入卷积通道分别进行卷积,也就是channel数量要保持一致,图片组这里只是堆叠放在一起表示而已)。
那么,如果要卷积后也输出多通道,增加卷积核(filers)的数量即可,示意图如下:
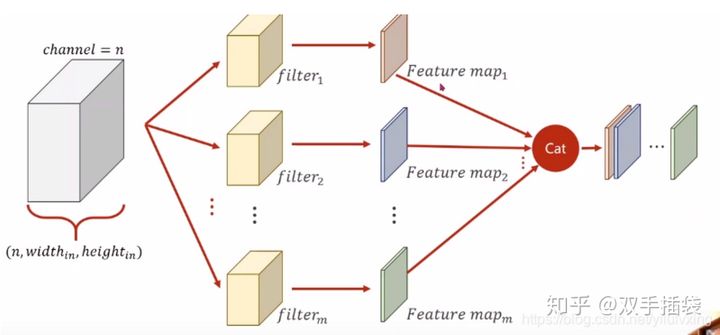
备注:上面的feature map的颜色,只是为了表示不同的卷积核对应的输出通道结果,不是表示对应的输出颜色